In 1978, the mathematician John McKay noticed what seemed like an odd coincidence. He had been studying the different ways of representing the structure of a mysterious entity called the monster group, a gargantuan algebraic object that, mathematicians believed, captured a new kind of symmetry. Mathematicians weren’t sure that the monster group actually existed, but they knew that if it did exist, it acted in special ways in particular dimensions, the first two of which were 1 and 196,883.

McKay, of Concordia University in Montreal, happened to pick up a mathematics paper in a completely different field, involving something called the j-function, one of the most fundamental objects in number theory. Strangely enough, this function’s first important coefficient is 196,884, which McKay instantly recognized as the sum of the monster’s first two special dimensions.

Most mathematicians dismissed the finding as a fluke, since there was no reason to expect the monster and the j-function to be even remotely related. However, the connection caught the attention of John Thompson, a Fields medalist now at the University of Florida in Gainesville, who made an additional discovery. The j-function’s second coefficient, 21,493,760, is the sum of the first three special dimensions of the monster: 1 + 196,883 + 21,296,876. It seemed as if the j-function was somehow controlling the structure of the elusive monster group.

Tanja Kernweiss

Miranda Cheng of the University of Amsterdam and France’s National Center for Scientific Research.

Soon, two other mathematicians had demonstrated so many of these numerical relationships that it no longer seemed possible that they were mere coincidences. In a 1979 paper called “Monstrous Moonshine,” the pair — John Conway, now of Princeton University, and Simon Norton — conjectured that these relationships must result from some deep connection between the monster group and the j-function. “They called it moonshine because it appeared so far-fetched,” said Don Zagier, a director of the Max Planck Institute for Mathematics in Bonn, Germany. “They were such wild ideas that it seemed like wishful thinking to imagine anyone could ever prove them.”

It took several more years before mathematicians succeeded in even constructing the monster group, but they had a good excuse: The monster has more than 10⁵³ elements, which is more than the number of atoms in a thousand Earths. In 1992, a decade after Robert Griess of the University of Michigan constructed the monster, Richard Borcherds tamed the wild ideas of monstrous moonshine, eventually earning a Fields Medal for this work. Borcherds, of the University of California, Berkeley, proved that there was a bridge between the two distant realms of mathematics in which the monster and the j-function live: namely, string theory, the counterintuitive idea that the universe has tiny hidden dimensions, too small to measure, in which strings vibrate to produce the physical effects we experience at the macroscopic scale.

Borcherds’ discovery touched off a revolution in pure mathematics, leading to a new field known as generalized Kac-Moody algebras. But from a string theory point of view, it was something of a backwater. The 24-dimensional string theory model that linked the j-function and the monster was far removed from the models string theorists were most excited about. “It seemed like just an esoteric corner of the theory, without much physical interest, although the math results were startling,” said Shamit Kachru, a string theorist at Stanford University.

Courtesy of John Duncan

John Duncan of Case Western Reserve University.

But now moonshine is undergoing a renaissance, one that may eventually have deep implications for string theory. Over the past five years, starting with a discovery analogous to McKay’s, mathematicians and physicists have come to realize that monstrous moonshine is just the start of the story.

Last week, researchers posted a paper on arxiv.org presenting a numerical proof of the so-called Umbral Moonshine Conjecture, formulated in 2012, which proposes that in addition to monstrous moonshine, there are 23 other moonshines: mysterious correspondences between the dimensions of a symmetry group on the one hand, and the coefficients of a special function on the other. The functions in these new moonshines have their origins in a prescient letter by one of mathematics’ great geniuses, written more than half a century before moonshine was even a glimmer in the minds of mathematicians.

The 23 new moonshines appear to be intertwined with some of the most central structures in string theory, four-dimensional objects known as K3 surfaces. The connection with umbral moonshine hints at hidden symmetries in these surfaces, said Miranda Cheng of the University of Amsterdam and France’s National Center for Scientific Research, who originated the Umbral Moonshine Conjecture together with John Duncan, of Case Western Reserve University in Cleveland, Ohio, and Jeffrey Harvey, of the University of Chicago. “This is important, and we need to understand it,” she said.

The new proof strongly suggests that in each of the 23 cases, there must be a string theory model that holds the key to understanding these otherwise baffling numerical correspondences. But the proof doesn’t go so far as to actually construct the relevant string theory models, leaving physicists with a tantalizing problem. “At the end of the day when we understand what moonshine is, it will be in terms of physics,” Duncan said.

Olena Shmahalo/Quanta Magazine

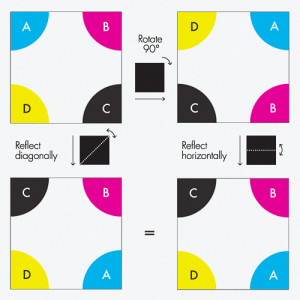
Rotating a square 90 degrees and then reflecting it horizontally has the same effect as reflecting it across a diagonal, so in the language of square symmetry arithmetic, 90-degree rotation + horizontal reflection = diagonal reflection.

Monstrous Moonshine

The symmetries of any given shape have a natural sort of arithmetic to them. For example, rotating a square 90 degrees and then flipping it horizontally is the same as flipping it across a diagonal — in other words, “90-degree rotation + horizontal flip = diagonal flip.” During the 19th century, mathematicians realized that they could distill this type of arithmetic into an algebraic entity called a group. The same abstract group can represent the symmetries of many different shapes, giving mathematicians a tidy way to understand the commonalities in different shapes.

Over much of the 20th century, mathematicians worked to classify all possible groups, and they gradually discovered something strange: While most simple finite groups fell into natural categories, there were 26 oddballs that defied categorization. Of these, the biggest, and the last to be discovered, was the monster.

Wikimedia Commons: Tom Ruen

Modular functions have repeating patterns related to the tiling above.

Before McKay’s serendipitous discovery nearly four decades ago, there was no reason to think the monster group had anything to do with the j-function, the second protagonist of the monstrous-moonshine story. The j-function belongs to a special class of functions whose graphs have repeating patterns similar to M. C. Escher’s tessellation of a disk with angels and devils, which shrink ever smaller as they approach the outer boundary. These “modular” functions are the heroes of number theory, playing a crucial role, for instance, in Andrew Wiles’ 1994 proof of Fermat’s Last Theorem. “Any time you hear about a striking result in number theory, there’s a high chance that it’s really a statement about modular forms,” Kachru said.

As with a sound wave, the j-function’s repeating pattern can be broken down into a collection of pure tones, so to speak, with coefficients indicating how “loud” each tone is. It is in these coefficients that McKay found the link to the monster group.

In the early 1990s, building on work by Igor Frenkel of Yale University, James Lepowsky of Rutgers University and Arne Meurman of Lund University in Sweden, Borcherds made sense of McKay’s discovery by showing that there is a particular string theory model in which the j-function and the monster group both play roles. The coefficients of the j-function count the ways strings can oscillate at each energy level. And the monster group captures the model’s symmetry at those energy levels.

The finding gave mathematicians a way to study the mind-bogglingly large monster group using the j-function, whose coefficients are easy to calculate. “Math is all about building bridges where on one side you see more clearly than on the other,” Duncan said. “But this bridge was so unexpectedly powerful that before you see the proof it’s kind of crazy.”

New Moonshine

While mathematicians explored the ramifications of monstrous moonshine, string theorists focused on a seemingly different problem: figuring out the geometry for the tiny dimensions in which strings are hypothesized to live. Different geometries allow strings to vibrate in different ways, just as tightening the tension on a drum changes its pitch. For decades, physicists have struggled to find a geometry that produces the physical effects we see in the real world.

David Kaplan, Petr Stepanek and Ryan Griffin for Quanta Magazine; music by Kevin MacLeod

Video: David Kaplan explains how the search for hidden symmetries leads to discoveries like the Higgs boson. (Watch all In Theory videos.)

An important ingredient in some of the most promising candidates for such a geometry is a collection of four-dimensional shapes known as K3 surfaces. In contrast with Borcherds’ string theory model, Kachru said, K3 surfaces fill the string theory textbooks.

Not enough is known about the geometry of K3 surfaces to count how many ways strings can oscillate at each energy level, but physicists can write down a more limited function counting certain physical states that appear in all K3 surfaces. In 2010, three string theorists — Tohru Eguchi of Kyoto University in Japan, Hirosi Ooguri of the California Institute of Technology in Pasadena, and Yuji Tachikawa of the University of Tokyo in Japan — noticed that if they wrote this function in a particular way, out popped coefficients that were the same as some special dimensions of another oddball group, called the Mathieu 24 (M24) group, which has nearly 250 million elements. The three physicists had discovered a new moonshine.

This time, physicists and mathematicians were all over the discovery. “I was at several conferences, and all the talk was about this new Mathieu moonshine,” Zagier said.

University of Chicago

Jeffrey Harvey of the University of Chicago.

Zagier attended one such conference in Zurich in July 2011, and there, Duncan wrote in an email, Zagier showed him “a piece of paper with lots of numbers on it” — the coefficients of some functions Zagier was studying called “mock modular” forms, which are related to modular functions. “Don [Zagier] pointed to a particular line of numbers and asked me — in jest, I think — if there is any finite group related to them,” Duncan wrote.

Duncan wasn’t sure, but he recognized the numbers on another line: They belonged to the special dimensions of a group called M12. Duncan buttonholed Miranda Cheng, and the two pored over the rest of Zagier’s piece of paper. The pair, together with Jeffrey Harvey, gradually realized that there was much more to the new moonshine than just the M24 example. The clue to the full moonshine picture, they found, lay in the nearly century-old writings of one of mathematics’ legendary figures.

Moonshine’s Shadows

In 1913, the English mathematician G. H. Hardy received a letter from an accounting clerk in Madras, India, describing some mathematical formulas he had discovered. Many of them were old hat, and some were flat-out wrong, but on the final page were three formulas that blew Hardy’s mind. “They must be true,” wrote Hardy, who promptly invited the clerk, Srinivasa Ramanujan, to England, “because, if they were not true, no one would have the imagination to invent them.”

Courtesy of Ken Ono

Srinivasa Ramanujan’s final letter to G. H. Hardy in 1920, explaining his discovery of what he called “mock theta” functions.

Ramanujan became famous for seemingly pulling mathematical relationships out of thin air, and he credited many of his discoveries to the goddess Namagiri, who appeared to him in visions, he said. His mathematical career was tragically brief, and in 1920, as he lay dying in India at age 32, he wrote Hardy another letter saying that he had discovered what he called “mock theta” functions, which entered into mathematics “beautifully.” Ramanujan listed 17 examples of these functions, but didn’t explain what they had in common. The question remained open for more than eight decades, until Sander Zwegers, then a graduate student of Zagier’s and now a professor at the University of Cologne in Germany, figured out in 2002 that they are all examples of what came to be known as mock modular forms.

After the Zurich moonshine conference, Cheng, Duncan and Harvey gradually figured out that M24 moonshine is one of 23 different moonshines, each making a connection between the special dimensions of a group and the coefficients of a mock modular form — just as monstrous moonshine made a connection between the monster group and the j-function. For each of these moonshines, the researchers conjectured, there is a string theory like the one in monstrous moonshine, in which the mock modular form counts the string states and the group captures the model’s symmetry. A mock modular form always has an associated modular function called its “shadow,” so they named their hypothesis the Umbral Moonshine Conjecture — umbra is Latin for “shadow.” Many of the mock modular forms that appear in the conjecture are among the 17 special examples Ramanujan listed in his prophetic letter.

Curiously enough, Borcherds’ earlier proof of monstrous moonshine also builds on work by Ramanujan: The algebraic objects at the core of the proof were discovered by Frenkel, Lepowsky and Meurman as they analyzed the three formulas that had so startled Hardy in Ramanujan’s first letter. “It’s amazing that these two letters form the cornerstone of what we know about moonshine,” said Ken Ono, of Emory University in Atlanta, Ga. “Without either letter, we couldn’t write this story.”

Finding the Beast

In the new paper posted on arxiv.org, Duncan, Ono and Ono’s graduate student Michael Griffin have come up with a numerical proof of the Umbral Moonshine Conjecture (one case of which — the M24 case — had already been proven by Terry Gannon, of the University of Alberta in Edmonton, Canada). The new analysis provides only hints of where physicists should look for the string theories that will unite the groups and the mock modular forms. Nevertheless, the proof confirms that the conjecture is on the right track, Harvey said. “We had all this structure, and it was so intricate and compelling that it was hard not to think there was some truth to it,” he said. “Having a mathematical proof makes it a solid piece of work that people can think seriously about.”

Emory University

Ken Ono of Emory University.

The string theory underlying umbral moonshine is likely to be “not just any physical theory, but a particularly important one,” Cheng said. “It suggests that there’s a special symmetry acting on the physical theory of K3 surfaces.” Researchers studying K3 surfaces can’t see this symmetry yet, she said, suggesting that “there is probably a better way of looking at that theory that we haven’t found yet.”

Physicists are also excited about a highly conjectural connection between moonshine and quantum gravity, the as-yet-undiscovered theory that will unite general relativity and quantum mechanics. In 2007, the physicist Edward Witten, of the Institute for Advanced Study in Princeton, N.J., speculated that the string theory in monstrous moonshine should offer a way to construct a model of three-dimensional quantum gravity, in which 194 natural categories of elements in the monster group correspond to 194 classes of black holes. Umbral moonshine may lead physicists to similar conjectures, giving hints of where to look for a quantum gravity theory. “That is a big hope for the field,” Duncan said.

The new numerical proof of the Umbral Moonshine Conjecture is “like looking for an animal on Mars and seeing its footprint, so we know it’s there,” Zagier said. Now, researchers have to find the animal — the string theory that would illuminate all these deep connections. “We really want to get our hands on it,” Zagier said.

This article was reprinted on ScientificAmerican.com.