dlhotson1.doc
Notes on
Dirac’s Equation and the Sea of Negative Energy by D.L. Hotson
http://openseti.org/Docs/HotsonPart1.pdf
Updated
8/02/12
Concise Summary
The Dirac Equation is the foundation for Quantum Electro
Dynamics, yet it was partially expunged, because it called for the existence of
not only positive energy positron-electron pairs, but also undetectable
negative energy positron-electron pairs,
forming what is called the
According to the author, it is also a Bose-Einstein Condensate.
The Dirac Equation, postulating only these four types of electrons, resolves all of the problems with the Standard Theory of particle physics, and provides simple, logical, and natural models of the electromagnetic field, the “photon,” the “strong nuclear” force, the Y wave, inertia, and gravitation. The “photon” is an electromagnetic wave, carried by electron-positron pairs, which have emerged from the sea of negative energy.
Preface
Dirac’s Equation and the
D.L. Hotson
Dirac’s Equation is profoundly important, and the Standard Model of particle physics is profoundly wrong. This paper addresses the nature of the energetic, non-stationary aether that Einstein missed, that Dirac’s Equation demonstrates, and that Heisenberg and others destroyed when they modified this equation.
The
treatment of Dirac’s equation is a lesson in the way modern science works (or
rather doesn’t). This treatment has more recently been paralleled by the
treatment of Reich, Pons and Fleischmann, Halton Arp,
and others.
Abstract
Dirac’s
wave equation is a relativistic generalization of the Schrodinger wave
equation.
His complete original equation describes a quantum spinor field, which has as solutions four different kinds of electrons; electrons and positrons of positive energy, and electrons and positrons of negative energy.
Such supposedly “fundamental” entities as quarks and gluons have no comparable wave equations; yet they wave. Therefore they cannot be truly fundamental. Since in principle the Dirac field comprises “everything that waves,” the equation therefore predicts that the entire physical universe can be made from these four kinds of electron.
In addition, direct applications of Dirac’s equation provide simple, logical, and natural models of the electromagnetic field, the “photon,” the “strong nuclear” force, the Y
wave, inertia, and gravitation. It provides direct-contact physical models that agree with experiment, as opposed to the purely mathematical models so much in vogue.
The
phase-entanglement feature of quantum mechanics, demonstrated by
banish causality. However, Dirac’s equation provides causal, direct contact models which are nonetheless non-local.
Yet Dirac’s original solutions to his equations were altered.
Introduction
(Problems with the Standard Model of Particle Physics)
Notes
principles for a successful theory:
The principle criteria for a successful scientific theory would
seem to be the following:
Criterion 1. Simplicity. It should embody as few “entities” as
possible, preferably only one. (This is William of Ockham’s
test, known as “Ockham’s Razor”: “Multiplicity ought not to
be posited without necessity.”)
Criterion 2. It should have few, preferably no, adjustable
parameters. (Also known as fudge factors.)
Criterion 3. It should be mathematically consistent.
Criterion 4. It should satisfy all of the known data, including
data unexplained, anomalous, or dismissed as “coincidence”
according to previous theories.
Criterion 5. It should obey causality: every effect should have
a proximate cause, with no “action at a distance.”
Criterion 6. It
should be falsifiable, making testable predictions
The author holds that all 6
criteria are violated by the current Standard Model of particle physics.
Criterion 1
The trend in science up until 1932
had been toward simplicity. Nonetheless around that time the simplifying trend reversed, and by the end of the
century, the accepted Standard Model (SM) of
particle physics called for around thirty-six
“fundamental” particles, most with an antiparticle,
and each with its very own “field”: again almost one
hundred separate entities, to generate three entities; the electron, proton,
and neutron, which are the building blocks of the 92 elements.
(Quantum Field Theory [QFT] in the SM is now so mathematically complex with its thirty-six or so [unobserved] fields that, as Treiman [2000] puts it, “There are no remotely realistic theories that are exactly soluble.”)
The universe
exhibits conspicuous economy,, even parsimony of
means. The DNA molecule; arguably the most complex
entity know, is built up from just four components.
Computer science
shows that unlimited complexity can be generated from just two binary
components.
Criterion 2
In contrast to the ideal of no adjustable parameters , the SM requires at least nineteen adjustable parameters.
Criterion 3
The SM is not mathematically
consistent. The SM calculations
of many ordinary values, such as the rest mass of the electron, come out to be
infinite. However, from experiment we know the electron’s rest mass to be 0.511
MeV.
To get rid of this “impossible result, “renormalization” is invoked: the positive infinity is, in effect, divided by a negative infinity. Since the result of this mathematically forbidden procedure is indeterminate, the desired value of 0.511 MeV is then simply entered by
hand.
Feynman,
who originated the “renormalization” process (with Schwinger and Tomonaga), himself called it a “. . .shell
game. . .Having to resort to such hocus-pocus has prevented
us
from proving that the theory of quantum electrodynamics is mathematically
self-consistent. . .[renormalization] is what I would call a dippy process!”
(Feynman, 1985) Asked for what he had won the Nobel Prize, Feynman replied,
“For sweeping them [the infinities] under the rug.” (Gleick,
1992)
The SM also has a major problem with mass. Gordon Kane (The Particle Garden, 1995) argues that the Standard Model should really be called the “Standard Theory” because it is nearly perfect— just a few minor flaws. He then goes on to mention one of them (p. 117):
“In its basic form, the Standard Theory is a theory for massless particles. All the leptons, quarks, and bosons must be particles without mass, or the mathematical consistency of the theory is destroyed. The photon and the gluons indeed have no mass, but the others
do.” If values for mass are just inserted into the equations, then calculations start to give infinite values for many ordinary measurements.
The current hope is that two more entities, the Higgs field and its supposed quantum, the Higgs boson, will somehow solve this dilemma.
[On July 4, 2012, an announcement was made of a possible discovery of the Higg’s boson. But how do we know this new particle is really fundamental, or just another piece of particle debris generated by the Hadron Super Collider? (HSC)? ]
The Equation
Pais (1994) ranks the spectacularly successful Dirac
Equation “. . .among the highest achievements of
twentieth-century science.” It was the first to be Lorentz-invariant, it had
electron spin as a necessary consequence, it gave the right magnetic moment,
the Thomas factor appeared automatically, and the Sommerfeld
fine structure formula was derived with the correct Goudsmit/Uhlenbeck
quantum numbers. At low energies, the results of the ordinary Schrödinger wave
equation are recovered. It predicted the positron, which was discovered by
Despite these successes, the physics community greeted it with alarm and outrage. This was because the equation gave twice as many states as they thought it should have. They
expected a Y with two components; but this equation gave four. After the discovery of the positron, it was realized that its four solutions call for electrons and positrons of positive energy, and electrons and positrons of negative energy (Pais, 1994).
As Dirac pointed out, this is because the energy-momentum- mass relation
E2 = c2p2 + m2c4
always associated with Einstein and Special Relativity has two roots; it calls for both positive and negative energy:
± E = (c2p2 + m2c4)1/2
[The mass-energy relationship E = mc2 was first derived and published by Oliver Heaviside (1890) and further refined by Poincare (1900), but Einstein (1905) first furnished the complete expression including momentum.] Dirac wondered what
to do with the negative energy solutions. “One gets over the difficulty on the classical theory by arbitrarily excluding those solutions that have a negative E. One cannot do this in the quantum theory, since in general a perturbation will cause transitions from states with E positive to states with E negative.” (Dirac, 1928a)
Since
all negative-energy states have lower energy than any positive-energy state,
Dirac wondered why there were any filled positive states, since
according to
entities tend to seek the
lowest-energy state. He suggested that all
of the negative energy
states must be filled, like the filled electron shells in the Pauli exclusion scheme. Then, unless a “vacancy” occurred, positive energy particles would “float” on the surface of the negative-energy “sea” and stay positive. Dirac’s “sea” of filled negative energy states, while it satisfied the equation, didn’t at all satisfy the physicists.
Heisenberg had developed the first successful version of quantum mechanics on a Machian basis, and an unobserved, ubiquitous “sea” was anathema. Worse, it harked back to an old war, the “aether” conflict. On largely Machian grounds, Einstein in 1905 had declared the “luminiferous aether,” the supposed carrier of light, to be unobserved, hence nonexistent.
[Lorentz’s electromagnetic aether (Lorentz, 1904, 1909) answered all of the other objections to a carrier of light, including the results of the Michelson-Morley experiment, so the only remaining objection was the Machian one.]
For a generation, the “Aether War” had raged in every faculty. By 1930 the tide was definitely running with the Relativists, and most remaining aether enthusiasts were dying out. (Lorentz, their doyen, died in 1928.) They were far from forgotten, however. Any
reference to a universal substance that undetectably filled space sounded too much like an aether.
The final argument was always that negative energy is impossible, with no imaginable physical meaning. Of course, pronouncements that something is impossible have a long history of looking foolish in retrospect, but this one seemed persuasive at the time.
Heisenberg’s
Window
The Dirac theory (1934) required every
charge to be surrounded by unlimited numbers of the opposite charged ends of
electron positron pairs (henceforth “epos”) from the negative energy sea.
Experiment has verified that the epos actually exist(ie, are not ‘virtual’, and are necessary. This “polarization of the vacuum”
has since become QED’s most celebrated success. Using difficult perturbation
calculations, the theory computes the electron’s magnetic “g” factor to an agreement
with experiment of ten significant figures or more.
Dirac used a “zeroth
order subtraction”, which in turn uses the Grassman
elements, to remove the two negative energy solutions to his equations, to
simplify calculations, but Heisenberg used this to deny the existence of such
negative states. Since the negative energy states were denied, the epos could
not come from them.
Therefore the operator that previously called
for unlimited numbers of negative energy electron positron pairs to be raised
in state (from negative to positive energy), now magically became a “creation
operator” of unlimited numbers of positive energy electron-positron pairs, without
any high-energy photons, or, indeed, any measurable energy input at all.
By not allowing negative energy states, the
concept of vacuum fluctuations around the zero baseline
evolved, or “zero point fluctuations”
The state-lowering operator magically
becomes an “annihilation operator,” producing no
high-energy photons or any other detectable energy. This
violation of energy conservation was excused due to a seeming “energy window,”
based on Heisenberg’s own uncertainty principle.
Thus, just as position and momentum of a
particle cannot both be known with maximal certainty, Delta Energy · Delta time .GE. h/2pi. He took this to mean that if Delta time
approaches 0, then the Delta energy approaches
infinity.
He therefore decided that these
“created” epos must be “virtual” rather than “actual,” though the equations
suggest no such thing.
One of the handy properties chosen for these
unlimited numbers of “virtual” epos is that, although formed of unlimited
amounts of energy, they somehow don’t gravitate, and thus violate General Relativity,
which states that such unlimited energy should curl the universe into a little
ball. Every electron, surrounded by unlimited numbers of epos, should be a
“black hole.”
As Dirac noted, physicists had always
arbitrarily ignored the negative energy solutions. If negative energy states
were real in some sense, as Dirac’s equation insisted, the physicists
had all been wrong all these
years, ignoring exactly half of reality. And that other half of reality,
alarmingly, seemed to resemble the anathematized aether.
The
Miracle of Creation
“Created” electron and positron spin energy
is real energy. It is the angular momentum
needed by the electron to set up a stable standing
wave around the proton, and is thus directly responsible for the extension and
stability of all matter. Instead of honestly facing this gross abandonment of
conservation of energy, current theory dubs particle angular momentum an “intrin-sic attribute, “ which means “we don’t know where
this energy comes from, so let’s not talk about it.”
Aside from the massive violations of energy conservation,
it seems hopelessly naïve to suppose that complex entities such as electrons
and positrons, with spin, charge, and a
number of other properties, could be “created out
of nothing,” even if the energy were available.
Wouldn’t it have made sense to look at what
the Dirac Equation mandates: instead of being “created,” electron-positron pairs
are merely raised in state from negative to positive energies.
When an electron approaches a positron, they
don’t just rush together and disappear. They approach until they are at a
distance equal to the electronic ground state of hydrogen. At this relatively
large distance they start to orbit around each other in the configuration
called “positronium.” After a short time they emit
two or more photons that total all of their positive energy, and are then no
longer detectable.
Conventional physics says that their charges
and spins have “cancelled” and that they have “annihilated” one another. But
doesn’t it make more sense to suppose that they still exist, as the Dirac
equation requires, merely lowered in state to negative energies?
Arp’s
Axiom
One wonders if there are any lengths to
which scientists will not go in order to save the reigning paradigm. In this
case, saving the paradigm would seem to involve the virtual abandonment of
science itself.
In this, they obeyed what we might call
“Arp’s Axiom.” The astronomer Halton Arp (1998) noted
that when facedwith a choice involving a paradigm
change, scientists will almost invariably choose the alternative that will save
the paradigm, regardless of the evidence.
A few scientists have looked at negative
energy: [H. Bondi (1957) Much later, he examined negative
energy within General Relativity. Also, T.E. Phipps, Jr. (1976, 1986) explores
both negative energy (the “hole theory”) and negative
(or “imaginary”) momentum in his “Beta Structure Hypothesis.”]
Evidence
that Heisenberg was wrong
Prof. S Treiman
shows (2000) that time may be considered quantized. If so, then it cannot be
taken in arbitrary increments approaching zero, so Heisenberg’s “ time window” doesn’t exist. But the reigning paradigm
escaped through that nonexistent window.
Symmetry
All through science, we observe almost total
symmetry between positive and negative. Charges come in positive and negative,
forces come in positive and negative, particles are
symmetric between matter and antimatter. This last
came as a great shock to physicists in the 1930s, but after it was accepted,
symmetry became the justification for many of our theoretical structures. Only
in energy do we deny that such a symmetry exists.
Science has ignored the negative energy
solutions to these equations as “imaginary,” like the square root of a negative
number. However, the square root of minus one is not “imaginary”— Mathematically, represented as i,
it simply designates a number field, or dimension, at right angles to the “real”
component. It is necessary to many
disciplines, especially electronics. In the Einstein- Minkowski
interpretation of special relativity this “imaginary” dimension is time.
Many of the popular string and superstring
theories require, for symmetry, a space of ten dimensions (Sirag,
2000). General Relativity as well calls for ten tensors, or “dimensions of
curvature” (Sirag, 1977a). To quote Dirac,
(1963), commenting on the ten tensors of
curvature of General Relativity, “The gravitational field is a tensor field with
ten components. One finds that six of the components are adequate for
describing everything of physical importance and the other four can be dropped
out of the equation. One cannot, however, pick out the six important components
from the complete set of ten in a way that does not destroy the
four-dimensional symmetry.”
[Recent studies in astronomy have shown that
space on a large scale is not curved, but appears to be Euclidean to the limits
of measurement (Arp 1998, Van Flandern 1998).]
In this case, General Relativity’s ten
tensors of curvature become merely linear degrees of freedom, or dimensions.
Dirac (1928a, b) laid the foundations of QED
with his relativistic wave equation. In doing so, though, Dirac found that
having three dimensions “real” and the fourth “imaginary” didn’t work—it
violated the symmetry. He took the first derivatives of all four dimensions by
introducing i as well into x, y, and z, making them
symmetrical by making them all “imaginary.” Most physicists have considered
this a trick, an “accident of the formalism,” and disregarded it.
“Imaginary” (orthogonal) directions give us
a place to put Dirac’s negative-energy “sea.” As we will demonstrate, it also
gives us a physical explanation of “negative energy.”
The Kinetic Theory of Mass/Energy
What is mass? Recent thought
suggests that the energy equation, instead of saying that two different things
can somehow be converted into each other, really means that mass is just
another form of energy (Haisch and Rueda, 1997)
Mass appears to be the
harmonic motion of charged particles “trapped” within an energy well of some
kind. This is why the most convenient and most often used unit expresses mass
in terms of energy
According to Haisch, Rueda, and Puthoff
(1994), mass is caused by an action of the Zero-Point Fluctuations (ZPF) of the
vacuum electromagnetic field that resists the acceleration of a harmonically
vibrating charge. “Mass is the manifestation of energy in the ZPF acting upon
[vibrating] charged particles to create forces.” (Haisch and Rueda, 1997) By this kinetic definition, an
electron-positron pair vibrating in a direction at right angles to our ordinary
four, an “imaginary” direction, would have negative
energy, the negative root of the Dirac equation. Just as the square root
of a negative number merely refers the result to a direction at right
angles to our ordinary directions, so the negative root of the energy
equation refers to an energy (a vibration of
charges) in one of these “imaginary” directions.
All of the groundbreaking
equations of quantum mechanics contain i either
explicitly or implicitly. The meaning of this has been staring us in the face
for seventy years. These “complex” functions involve vibrations partly in
“real” partly in “imaginary” directions. (And some that are “pure imaginary,”such as the ±c velocity eigenvalue of the
electron/positron.)
The
Electron Positron Pair
The negative energy electrons and positrons called
for in Dirac’s Equation, appear to be permanently
associated in pairs-epos. According
to Dirac’s theory, when an
electron and positron combine, they do not annihilate one another, nor do they
even come very close together, but rather orbit on another as an entity called
a “positronium.”
They drop into the negative energy sea. What
configuration do they assume in the negative energy sea?
Dirac’s equation describes a
“spinor field.” In such a field, rotation of the wave
function through 360° does not get it back to its original state, but to its
opposite: the electron has to “turn around twice” to get back to where it was.
At 360°, its wave function Y becomes -Y, and it becomes, in effect, a positron travelling backwards,
In QED, a positron is
considered to be an electron travelling backwards in time [Feynman, 1985].) So
a positron is really only a totally out-of-phase electron.
The equation also says
(Huang, 1952) that the electron has an internal vibrational velocity of ±c. Since the electromagnetic wave is
the only momentum-carrying entity allowed to travel at
c, this could mean that this internal vibration is as an electromagnetic
wave.
The resultant orbiting
electron-positron pair might then be configured as vibrating in an imaginary
direction while turning into each other every 360°, so they would be
“particles” at 0°, 360°, and 720°, and waves in between (“wave-particle
duality”).
The period of this
reciprocation would have to be the “quantum of time,” t, equal
to 2e2/3mc3, or 6.26 x 10-24 seconds. This is
the time required for an “appreciable change” in the wave equation, which therefore
only changes in increments of t. This is G e, the
Lorentz-Abraham damping
constant of the electron, and in classical electrodynamics, it is called the
“damping constant” or the “characteristic time” of the electron.
In particle physics, this is the
minimum time taken by any interaction, and interactions
that take longer than this seem
to require exact multiples of this “quantum of time.” Since they travel at c
as electromagnetic waves, this would make the “length” of an epo (a one-dimensional string, with a “point particle” at
each end) equal to tc, 2e2/3mc2,
or 1.87 x 10-15 meters. This is the measured diameter of the proton,
which, is not a “mere coincidence.”
Considering negative energy to be an
imaginary component (be at “right angles” to the real quantities) is consistent
with the fact that
the electron’s wave function is a complex variable, with “real” and
“imaginary” parts, and with the fact that the electron’s angular momentum is
also complex.
The
Quantum Field
In his book The Odd
Quantum, Sam Treiman (2000) introduces a very
simple “model field”: a single, scalar field f (x,y,z,t) which classically obeys the linear
differential equation:
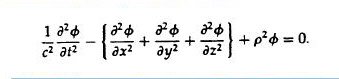
He then goes on to quantize
the field, and solve for the eigenvalues. He finds that the allowed momentum
eigenvalues p form a continuum, and for any given momentum p there
is a particular state with energy
E
= [(cp)2 + (mc2)2]1/2,
where m = hp/c.
“This is just exactly the
relativistic energy-momentum relation that holds for a material particle of
mass m.” [The above expression should
read “plus or minus E.” The one-particle state can have either positive
or negative energy.]
The remarkable thing is that,
starting with a simple field, particles emerge
as quanta of the field.
This particular “model
field,” deliberately chosen for its simplicity, describes as its quanta neutral,
spin-zero bosons.
It turns out that this simplest possible quantum field would necessarily be
populated with all possible numbers of strictly identical, neutral,
spin-zero bosons: Gribbin notes (1998b), “In the quantum world a field must give rise to particles.”
No such field of unlimited
numbers of neutral, spin-zero positive-energy bosons exists.
However, as we have argued
above, a “sea” of negative-energy, neutral, spin-zero bosons is a
requirement of quantum mechanics itself: of
the energy equation, and of the Dirac equation of the
electron.
Two of the Dirac Equation solutions call for negative-energy electron-positron pairs, which would necessarily associate as neutral spin-zero bosons.
We have now approached this from three different directions, and they all point to the same result.
In this model field there are no
interactions; it is called
a free field theory.
Start with a state in which two particles
approach as for a collision, and in fact they
won’t collide (because both electron and positron
are waves at this time) because the classical field equation on which it is
based is linear: the sum of any set of solutions is also a solution.
(For this reason, quantum field theory, with
its multiple fields, one for each “fundamental” particle, requires non-linear terms
in the differential equations that describe them in order for there to be
interactions, and this is why none of the theories are exactly soluble.)
In laboratory ultra-cold studies, we remove
“positive” energy and achieve lower temperatures to come closer and closer to
“zero absolute,” a state of no positive energy.
Apparent energy and activity decline rapidly
as temperature drops. One would think that at temperatures near absolute zero
matter would lose its cohesion and fall apart.
But as we approach the zero-point, some
curious things happen. First, centered at about 2.73°K, we find an immense
number of photons. At 0°K, the equations of QM tell us that there is immense
energy (hv/2).
Bose-Einstein
Condensate
Matter binds closer and closer together
until at even lower temperatures the individual molecules function as a single
unit; ie a Bose-Einstein Condensate, in which
superconductivity and superfluidity occur. These are
very energetic states, in which negative (binding) energy has overcome the tiny
residual positive (freeing) energy, so that all particles are all governed by
the same wave function.
The author suggests that the negative energy sea of bosons
(epos) called for by the equations must exist in the form of a BEC. According
to the equations and everything
we know, our reality is surrounded by and
immersed in a vast, all pervasive Bose-Einstein Condensate.
This is supported by
Non-local or faster than light action also
must be a property of the electromagnetic field, according to a whole series of
experimental results starting with the Sherwin-Rawcliffe
experiment (1960) and continuing with those of the Graneaus (1982, 1983, 1985, 1987, 1993) and Pappas (1983, 1990A,
1990B). These experiments all show that changes in
the electromagnetic field must propagate nearly
instantaneously, so that a moving charge has no “left-behind potential hill.”
The same is true of gravitation, as was
shown in the classical Laplace demonstration based on the absence of any change
in the angular momentum of the earth’s orbit (Laplace, 1966), and as has been
repeatedly demonstrated by Van Flandern (1993, 1996,
1998). He shows that even in a static field, propagation of gravity merely at light
speed
would result in a “couple,” which would
measurably increase the earth’s angular momentum. He further shows that General Relativity, supposed
to be a local theory, nonetheless assumes and requires instantaneous changes in
the “curvature of empty
space,” and so is non-local.
The BEC is apparently the only extended structure
that exhibits this non-locality. If you
insert an electron into one end of a BEC, however large, an electron emerges
from the other end faster than light can travel that distance—this is the
phenomenon of superconductivity
These non-local actions are not literally
instantaneous, but take the finite time tau.
We have looked at three equations, the energy
equation, Dirac’s equation, and this very simplest quantum field, which we
might call the “Zeroth Quantum Field” (ZQF). Each of
them seem to be describing this same object, a universal BEC negative energy “sea”
composed of unlimited numbers of spin 0 neutral negative-energy bosons, which
have to be one-dimensional electron-positron pairs.
Physics
Through the Looking Glass
That there is a negative-energy “sea”
balancing the positive energy of our reality restores the symmetry between
negative and positive energy called for by the energy equation and
Dirac’s equation. Moreover, there are indications that
negative energy is primary.
The
Electromagnetic Field
An ionic electron must instantly be
surrounded by a sphere of the positron ends of polarized epos, as has been
verified by experiment. The positrons must form a sphere of diameter tau c. But
this takes no energy, since in the infinite sea there is already a positron and
an electron at the exact points necessary to make that sphere of polarized
epos, each radial to the ion. The only
difference is that these are now positive energy epos, as their vectors point
in real directions.
Each positron in the inner sphere has a
potential induced by the ionic electron.
This would unbalance the epo,
inducing a potential between the positron and its electron,
which would again force the electron end to
polarize another epo, and so on indefinitely, forming
chains of polarized epos. These chains would continue into space until they
terminated at a charge of opposite polarity, as in Figures 1 and 2
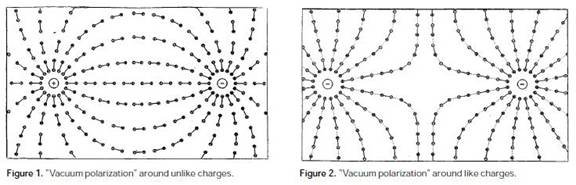
Charge is carried by proxy by these chains
of epos. The strength of the charge measured anywhere would vary as the inverse
square of the distance, as the Coulomb gauge requires. (This strength would be
measured in “epo chains per unit area,” just as
Faraday would have us measure “lines of
force per unit area.”)
Since this pattern duplicates every aspect
of the electromagnetic field, we submit that this IS the
electromagnetic field, much as Faraday or Maxwell would have drawn it, with
Faraday’s “lines of force” exactly duplicated by chains of epos. The epos are the quanta of the EM field.
In this “epo
model,” the “tension along the lines of force” is supplied by the attraction
between the aligned unlike charges in the epo chains.
The pressure in all directions at
right angles to the epo
chains is supplied by repulsion between the like charges in different chains
lined up roughly parallel to each other. This also accounts for the repulsion between
like charges of “real” ions, as seen in Figure 2.
Further, we note that what had been taken to
be a mathematical abstraction, the “electromagnetic field,” now has a definite
physical reality.
Conservation
of Angular Momentum (aka the Photon)
As a single electron of hydrogen orbiting
the proton at some energy level above its ground state jumps to its ground state, it must lose
angular momentum—spin—in the
amount of hv. In the conventional view, the electron “emits”—instantly
creates—a “particle” called the “photon,” which is an electromagnetic “wavicle” traveling at velocity c, which delivers the angular
momentum intact to some other electron and then vanishes.
Since Einstein banished the aether, however, the question has been “what is waving?”
The photon has no rest mass, and contains no charges—so it violates our kinetic
definition of energy.
In order for a “real” object to get rid of
spin angular momentum in the macroscopic world, that real object must set some
other real object spinning. The author holds this to also be true in the
macroscopic world: what is more natural than that it set spinning those objects
closest to it, the polarized epos that surround it? They have charges, and are
pointing in “real” directions, so they can absorb the “real” (positive) spin
energy that the electron has to get rid of.
When the electron goes to the ground state, the epos are left
“holding the spin.”
[some more than
others, because the lost spin is a vector quantity, and its energy will go
primarily to epos that are pointing in the vector direction. ] The epos are no
longer in chains, and the spin energy will travel
up the epo “string” (at velocity c)
The “photon” at this point would be a wave,
carried by epos, which can be termed an epho.
Feynman could not explain why
a “path” should have phase, he merely asserted
that it did. We can now see that
it has phase because each epho on each “path” is
itself an electromagnetic wave with phase. Together they form a coherent wavefront. Ephos on the “least action”
path will reinforce each other, and any epho that
takes a “wild” path gets out of phase with the wavefront,
suffers destructive interference, its angular momentum is cancelled, and it
drops back into the epo “sea.” Thus the only ephos that continue to carry energy are those that are
close to the (least action) “classical” trajectory.
In the famous “two slit”
experiment, many of the paths comprising the epho
“wave” which represents the “single photon” go through each slit, and interfere
with each other, forming the well-known Y wave “interference pattern.”
At the screen, one of them is randomly selected according to |Y|2,
the probability, to deliver all of the
wave’s angular momentum to a single
electron in the screen.
This amounts to an analog-to-digital
conversion, with the sum of the angular momentum of the entire wave being delivered
to a single electron, a “point event.”
Note that this model gives
physical meaning both to Feynman’s path integral version of QM and to the Y wave. Further,
it should be noted that since each epho wave
individually travels at c, the velocity of light would be independent of
the velocity of the source, and the same in any frame of reference. It would in
fact be Lorentz’s electromagnetic aether (Lorentz,
1909). The transmission of light would agree with
Lorentzian relativity, which meets all
the tests devised for Special Relativity (Ives, 1946, 1949, 1950, 1951),
including those that SR fails, such as the Sagnac
effect (Sagnac, 1913) and the Silvertooth
effect (Silvertooth, 1987, 1989, Silvertooth
and
Whitney,
1992).
Related articles: